Teorema de Ángulos Inscritos Fórmula y Ejercicios Neurochispas
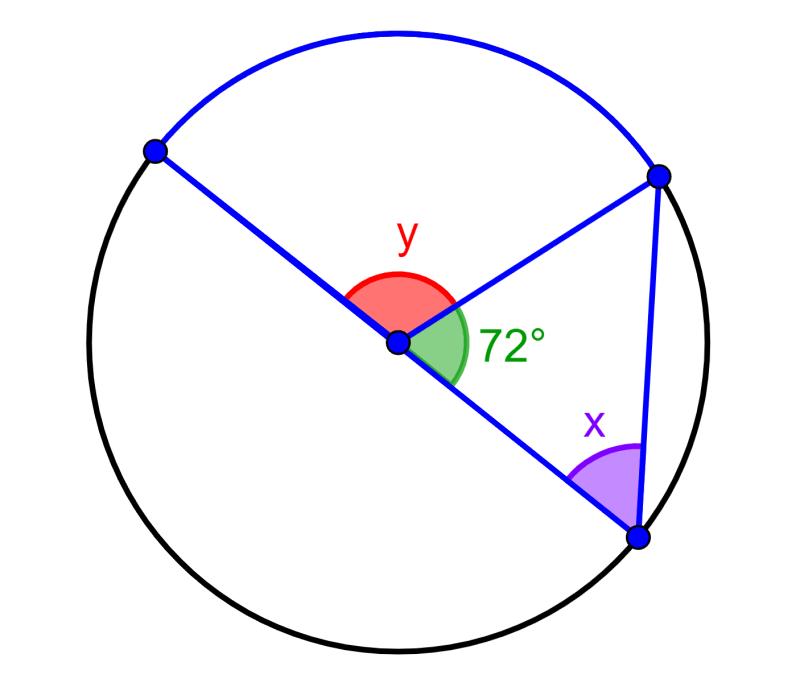
Lo que vamos a demostrar. 50 ∘ 25 ∘. Demostraremos que algo interesante sucede cuando un ángulo inscrito ( ψ) y un ángulo central ( θ) intersecan al mismo arco: la medida del ángulo central es el doble de la medida del ángulo inscrito. θ = 2 ψ.
Ángulo central en un círculo Tutorela

La fórmula del ángulo exterior viene dada por. Angulo exterior, ∠BUENA = ½ (b - a) Trabajemos en algunos ejemplos: ejemplo 1. Encuentre el ángulo central de un segmento cuya longitud de arco es de 15.7 cm y su radio es de 6 cm. Solución. Ángulo central = (longitud del arco x 360) / 2πr. Ángulo central = (15.7 x 360) / 2 x 3.14 x 6.
Angulos de la circunferencia
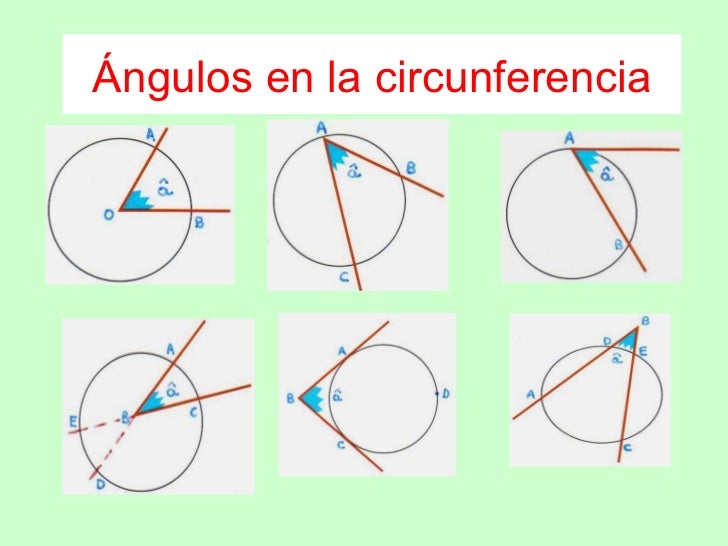
El ángulo es un ángulo inscrito. Dibujamos el segmento y lo alargamos hasta que interseque la circunferencia en el punto . El ángulo subtiende el arco . Supongamos que el centro de la circunferencia está fuera del ángulo . Por lo tanto el arco no incluye el punto , ya que es el punto diamentralmente opuesto a .
Ángulos en la circunferencia │ ángulo central YouTube

Un ángulo inscrito es la mitad de la medida de un ángulo central subtendido por el mismo arco . Un ángulo central es el doble de la medida de un ángulo inscrito subtendido por el mismo arco. COB ya que ambos están subtendidos por arc (CB).
Álbumes 103+ Foto Angulos Inscritos Y Centrales De Un Circulo El último
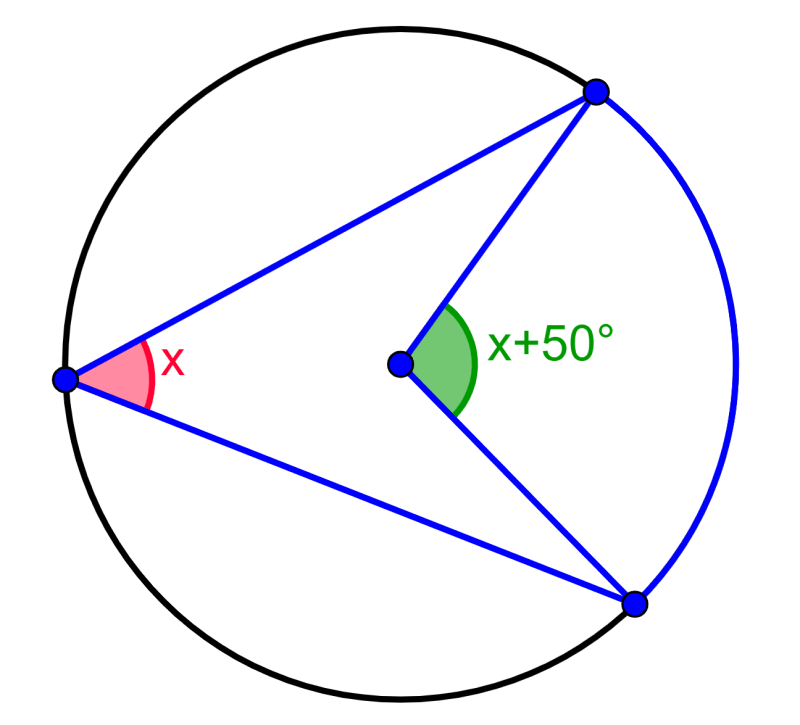
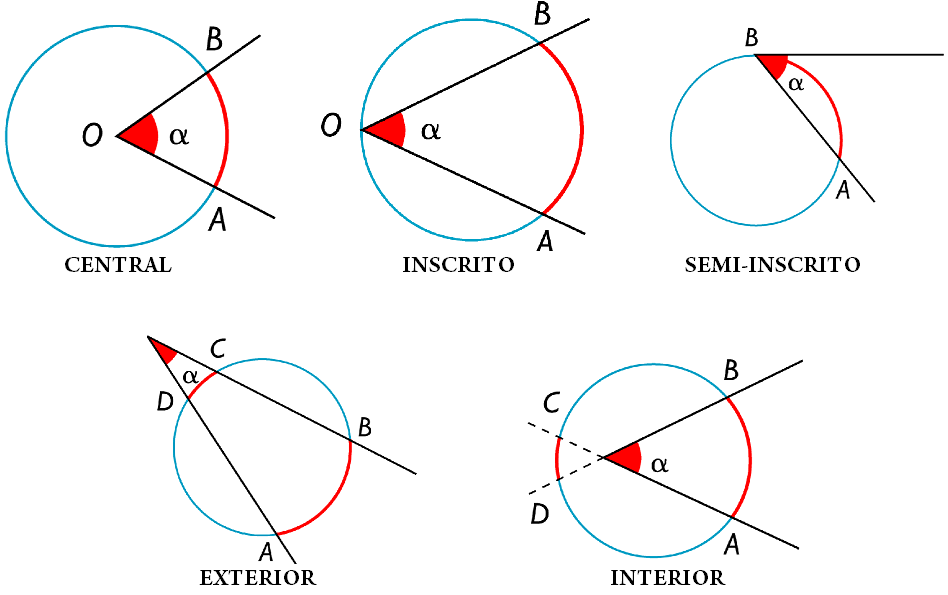
Figura 1. Los tipos de ángulos en la circunferencia son: el central, el inscrito, el exterior y el interior. Fuente: F. Zapata. 2.-. El ángulo inscrito, cuyo vértice está sobre la circunferencia y sus lados son secantes o tangente a la circunferencia. 3.- Ángulo exterior, cuyo vértice está fuera de la circunferencia pero sus lados son.
6. angulos y arcos en la circunferencia
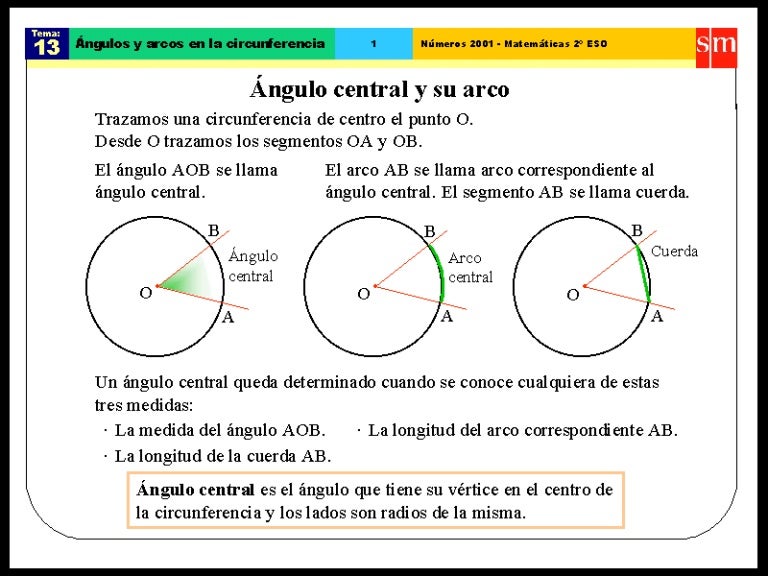
El ángulo central ∠AOB asociado al diámetro es un ángulo plano, cuya medida es 180º. De acuerdo al teorema 1, todo ángulo inscrito en la circunferencia que subtiende la misma cuerda (en este caso el diámetro), tiene como medida la mitad del ángulo central que subtiende la misma cuerda, que para nuestro ejemplo es 180º/2 = 90º. Figura 9.
2. Ángulo inscrito en una circunferencia YouTube

Mencionamos que un ángulo inscrito es un ángulo cuyo vértice está sobre el círculo, es decir, sobre la circunferencia. y cuyos extremos son cuerdas en un círculo. Por lo tanto, si traza dos cuerdas cualesquiera en un círculo, se encontrarán en el mismo punto de la circunferencia - Sobre el círculo mismo, crearemos un ángulo. El.
Álbumes 103+ Foto Angulos Inscritos Y Centrales De Un Circulo El último

El Teorema del Ángulo Inscrito establece que la medida de un ángulo inscrito es la mitad de la medida de su arco interceptado. Figura 6.14.2 6.14. 2. m∠ADC = 1 2mACˆ m ∠ A D C = 1 2 m A C ^ y mACˆ = 2m∠ADC m A C ^ = 2 m ∠ A D C. Los ángulos inscritos que interceptan el mismo arco son congruentes. Esto se llama Teorema de Ángulos.
Angulos de la circunferencia
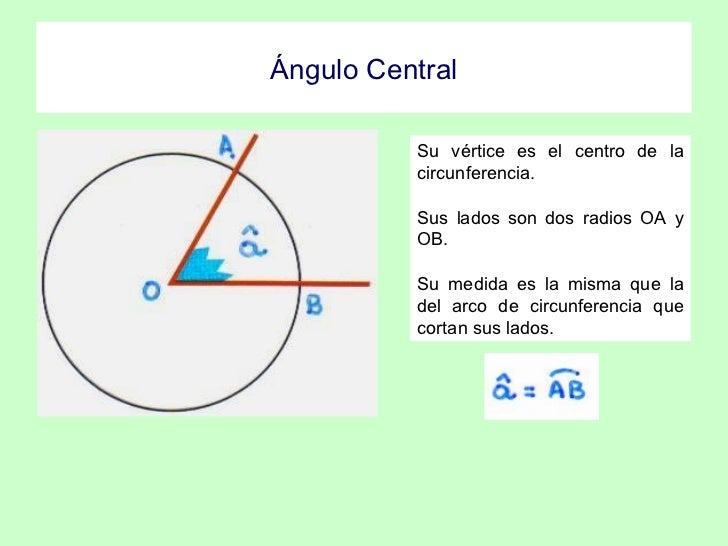
Ángulo inscrito : Llamaremos ángulo inscrito en una circunferencia a todo ángulo convexo cuyo vértice es un punto de la circunferencia y sus lados secantes a ella. Ángulo central : Llamaremos ángulo central en una circunferencia a todo ángulo cuyo vértice es el centro de esta. Analicemos si existe una relación entre un ángulo inscrito.
Álbumes 103+ Foto Angulos Inscritos Y Centrales De Un Circulo El último
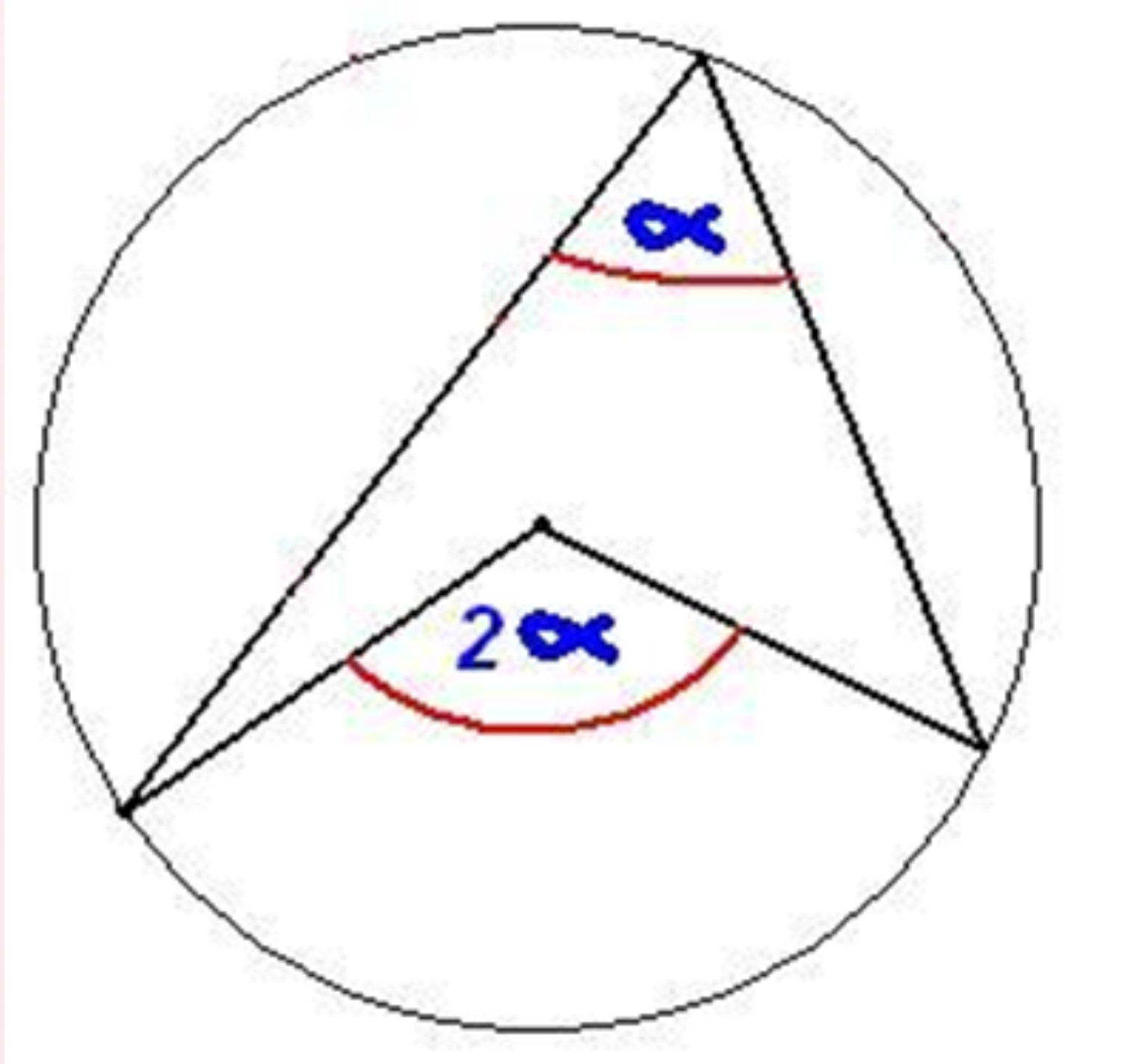
Supongamos que conocemos la medida de un ángulo inscrito en un círculo, que es de 45 grados. Para calcular la medida del arco correspondiente, aplicamos la relación establecida previamente: el arco tendrá una medida de 90 grados, ya que es el doble de la medida del ángulo inscrito.
Ángulo central en un círculo Tutorela
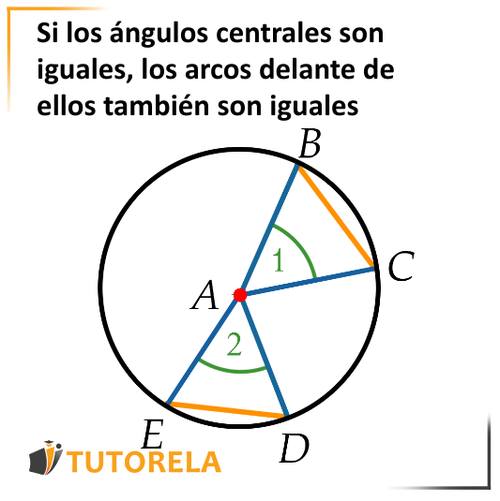
Es importante notar que dos puntos, A y B, sobre una circunferencia determinan dos arcos y, por tanto, dos ángulos centrales: uno cóncavo (α = 130,68º) y. uno convexo (β = 229,32º) , o los dos iguales, que sumarán 360º . Los ángulos inscritos ( γ = 65,34º y δ = 114,66 en la figura abajo) que subtienden los mismos arcos que.
Ángulo central en un círculo Tutorela
Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más. Khan Academy es una organización sin fines de lucro, con la misión de proveer una educación gratuita de clase mundial, para cualquier persona en cualquier lugar.
ÁNGULOS INSCRITOS EN UNA CIRCUNFERENCIA GeoGebra

Propiedades de los ángulos inscritos y centrales en un círculo. Los ángulos inscritos en un círculo son aquellos cuyos vértices se encuentran sobre la circunferencia, y sus lados son secantes o cuerdas de la circunferencia. Por otro lado, los ángulos centrales tienen su vértice en el centro del círculo y sus lados son radii del círculo.
Valor de un Angulo Inscrito en una Circunferencia GeoGebra
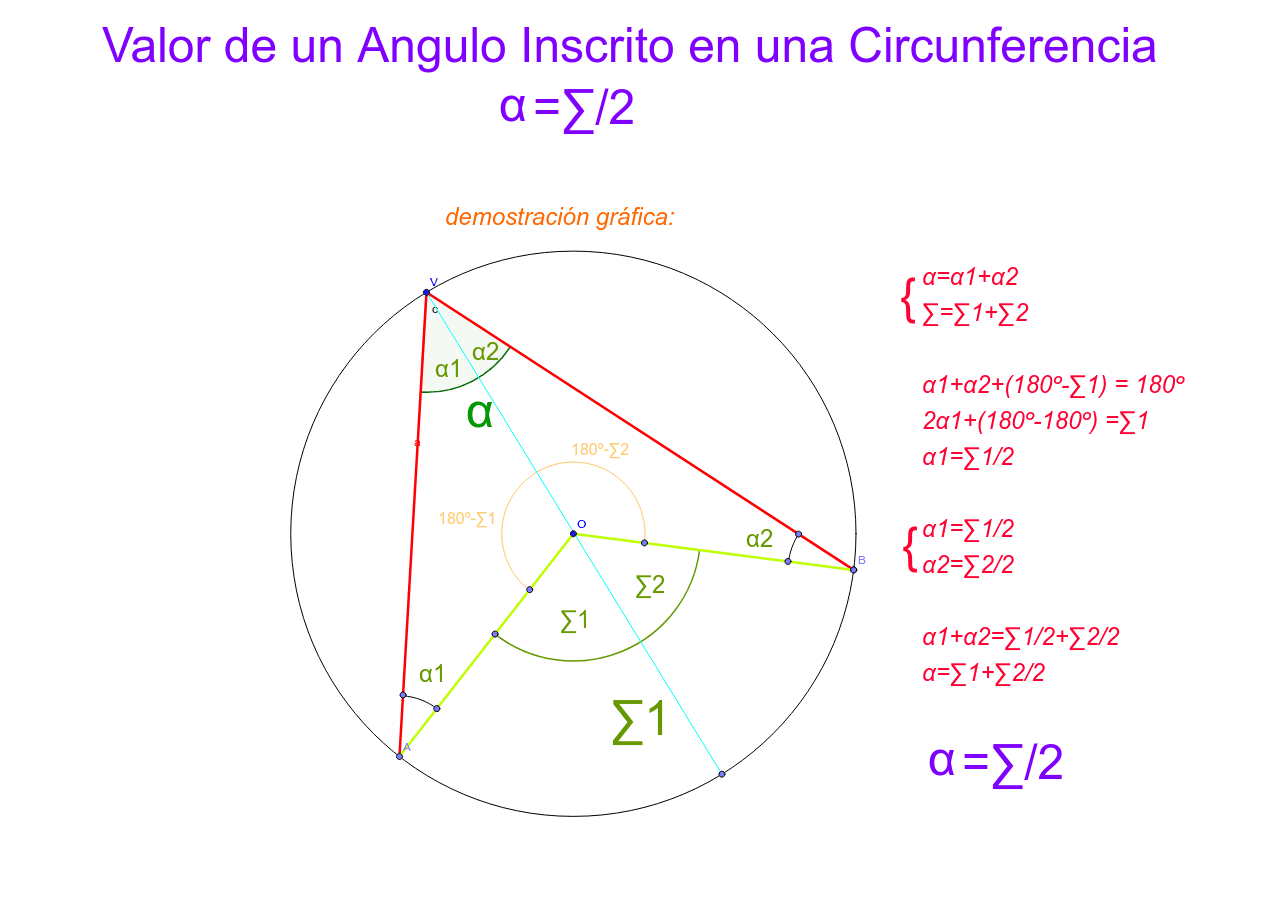
Ángulo central e inscrito en una circunferencia. Dados dos puntos en una circunferencia, los radios desde el centro de la circunferencia a esos dos puntos forman un ángulo central. Un ángulo inscrito es un ángulo subtendido en un punto de la circunferencia por otros dos puntos de la circunferencia. Un ángulo inscrito está definido por dos.
Aprendamos de la Circunferencia Ángulos en una circunferencia
Resumen de la lección. En resumen, el ángulo central en un círculo es el ángulo formado por dos líneas de radio. Un ángulo inscrito es el ángulo formado por puntos en la circunferencia del círculo. Hay algunas cosas clave que debe saber sobre los ángulos centrales e inscritos.
Ángulo inscrito en una circunferencia con ejemplos incluidosnivel básico YouTube

Ángulos inscritos Un ángulo inscrito es un ángulo hecho de dos rectas secantes de un círculo que se intersectan en un punto en el círculo. En la figura mostrada, es el ángulo inscrito. Una propiedad básica de un ángulo inscrito es aquella que el arco interceptado del ángulo tiene exactamente el doble de la medida del ángulo inscrito.